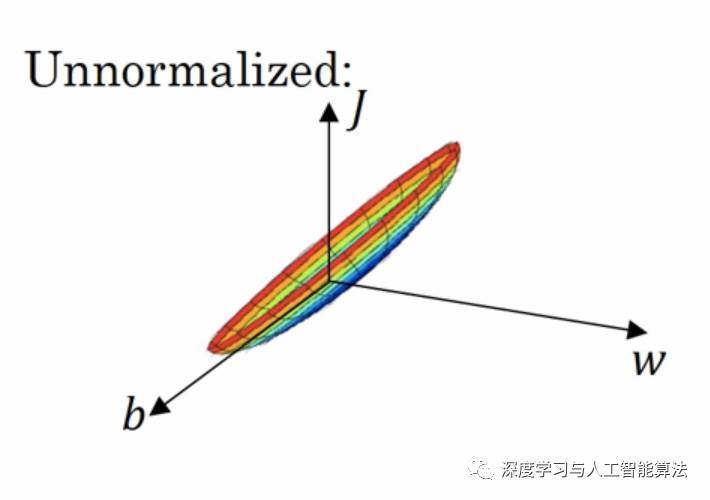
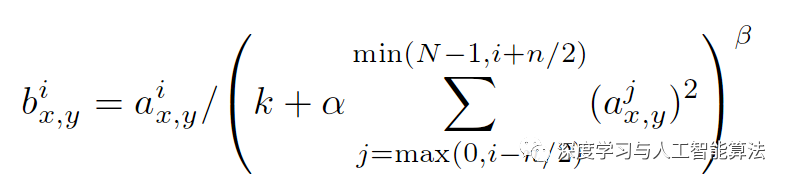The author of this article is original, please indicate the source. Today we are going to explore the importance of input normalization, also known as standardization. Input normalization is a technique that originated from the paper by Krizhevsky and Hinton on ImageNet. It's essentially a form of local normalization used to improve the training process in neural networks. In real-world applications, data often comes in different dimensions or with varying feature distributions. Imagine a scenario like the one shown below: Such data can make training more challenging. Let’s take a look at what the gradient descent landscape might look like in this case. As you can see, the shape is long and narrow, which makes the optimization process slow and inefficient. To address this issue, we apply input normalization. Here's the formula used for this purpose: Using this formula, the gradient descent becomes more balanced and efficient, as shown below: This means that no matter where you start the gradient descent, the convergence is similar, leading to faster and more stable training. Now, let’s see how this is implemented in TensorFlow. The API used is `tf.nn.local_response_normalization`, which is also known as `tf.nn.lrn`. Here’s how the function is defined: There are several parameters in this function. Let's break them down. The `input` is the tensor you want to normalize. `depth_radius` corresponds to n/2 in the formula. You might wonder why it's called `depth_radius` instead of just `radius`. Well, this parameter defines the number of neighboring channels to consider during normalization, hence the term "depth." The `bias` parameter adds an offset to prevent division by zero, `alpha` scales the normalization factor, and `beta` controls the exponent in the denominator. In essence, LRN can be thought of as dividing each pixel by the sum of the squares of other corresponding pixels within a certain radius. This helps in normalizing the activations across different channels. Let’s look at an example to see how this works in practice. The output for `a` is: And the output for `b` after normalization is: Circuit Breaker Rocker Switches Circuit Breaker Rocker Switches Gray,Circuit Breaker Rocker Switches Black,Circuit Breaker Rocker Switches Black White,Circuit Breaker Rocker Switches Blue Yang Guang Auli Electronic Appliances Co., Ltd. , https://www.ygpowerstrips.com